Topinformationen

Welcome to Klaus Brauer's SOLITON Page

One of the most exciting phenomena in dealing with non-linear Partial Differential Equations are the Solitons or Solitary Waves. The first person reporting these phenomena was the Scottish engineer John Scott Russel, who described the propagation of a wave in shallow water. Nowadays we have better knowledge of the underlying mathematical properties. Solitons are the solutions of the famous non-linear Korteweg-de Vries Equation. Solutions to this PDE can be found in using the method of Bäcklund transform.

Korteweg - de Vries Equation:

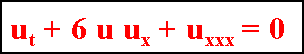
It is possible to construct solutions to the Korteweg - de Vries equation which are non-linear superpositions of regular and irregular single solutions.

The interested reader is referred to the book:

Vvedensky, Dimitri D.
    Partial Differential Equations with Mathematica - Chapter 9
    Addison-Wesley Publishing Company, Reading, MA, ISBN 0-201-54409-1, 1993.

The solution may be visualizied as a 3D Plot and as a Density Plot (both generated with Mathematica 9.0.1).
Finally it can be nicely observed by looking at the animated graphs, produced as well with Mathematica, Version 9 (available since 2013).

The author of this Web page has written an article (23 pages as a PDF file, Update: February 2014). The contents points out to some history, presents Vvedensky's solutions shows some Mathematica code and presents some graphical results.

• KdV.pdfThe Korteweg-de Vries Equation: History, exact Solutions, and graphical Representation

The construction method has been performed for one solution as well as for two and for three superpositioned solutions. Each of them have a parameter, say β₁ for the one soliton solution resp. β₁ and β₂ for two waves or β₁, β₂ and β₃ for three waves.
The effect is that a wave travels the faster the greater that parameter is  - thus overtaking a slower wave. The two or the three waves preserve their shapes even after the overtaking process.

Analytical Solution and graphical representation for the One Soliton Solution

Analytical Solution and graphical representation for the Two Solitons Solution

Analytical Solution and graphical representation for the Three Solitons Solution

Further Information:

• A lot of information including the revival of John Scott Russel's experiments is given by  Heriot-Watt University (Edinburgh/Scotland)
• The University of Kyoto/Japan has prepared a Soliton-Lab Art Gallery
• Further Information, especially on the Sine-Gordon-Equation, solved by using the Computer Algebra System Maple, is coming from Tver State University in Russia, look at the page of Andrey E. Miroshnichenko
• In another nice article Mathematica is used again but the graphics have a different "look & feel", the author gets solutions by using numerical methods with Mathematica - watch Young Physics from California
• Lots of Links may be found from R. Victor Jones' Soliton Page
• Even a German TV channel has brought solitons to the public.
• Real solitons observed in the Strait of Gibraltar